Understanding mission capabilities, needs, wants and clearances.
One of the most important aspects of starting any project is to ensure that you have the scope, breadth, purpose and principle of the project clear. You see, as you work on a project, hindsight is 20-20, but, budgets, constraints, space in the actual craft and in facilities starts running low. Not to forget, that as human you have a limited amount of time you can spend on something, and limited patience to deal with something day-in and day-out.
To ensure that a project goes without hitch, and without significant over-runs of money, time, resources or humans(in-case you get frustrated and vehicular manslaughter is your way coping with it), one must study and define the principles rather than the problem statement. So far, defining the purpose and principle of a project is important. This gives the equation:
![]()
Unfortunately, this equation does not show the full picture, because there is an infamous spiral, a rabbit hole that will lead you to a world of regret. Often called the “Design Spiral” , it will suck the life out of you if you do not pay attention to the way you are planning your project out. (Aerospace is a deadly mistress, and she only wants your life, not half your money)
One of the many solutions I found to making this work, was to use a “semi-parametric” approach to the design and the optimization part of the process. Another important factor one needs to consider is the amount of time and money you are willing to sacrifice for this endeavor. And additionally remind yourself why you are doing this. It is often, quite easy for someone to give up due to frustration, and with a million different software, libraries and additional analysis parameters, not to forget languages and frameworks like LATEX and FORTRAN do not make it easier.
Another fun thing about using a semi-parametric approach was to use linear algebra concepts, specifically Jacobians and residuals. Although numerical analysis sounds like overkill for a basic project, it is useful, and once you understand the beauty of it, you will find that the topic is useful for more than just making planes fly or make you fear math.
The Jacobian matrix is a function that maps a vector of input variables to a matrix of partial derivatives for a vector-valued output, such that ![]() , where m is the number of outputs and n is the number of inputs.
, where m is the number of outputs and n is the number of inputs.
All it means is; if you have two functions ![]() and
and ![]() with the variables
with the variables ![]() and
and ![]() then the Jacobian Matrix J would be:
then the Jacobian Matrix J would be:
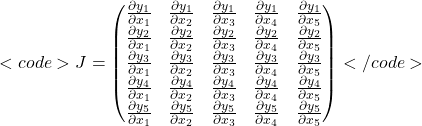
As you can see, a Jacobian is a pretty sweet operation, because it gives you the rates of the rates of change of the function with respect the rates of change of each variable in between the functions. Remember that, a Jacobian is the rate of change in two different functions, or at least, functions that are significantly different than the other.( yes, I know, in trying to dumb it down, I made it a tongue twister. I guaranteed a funny way to make heavy lift aircraft, not a straight read manual. It’s my way way living upto my Ikea ambitions). The Jacobian is like a lathe that carves using a template. On one side you have square block of wood, and on the other you have a vase, the lathe then mirrors the shape on the square block, using the fully made vase as a template. A vase is curved, and that’s important, because orthogonal shapes can be whole numbers and these need elementary row operations, not derivatives.
Anyway, Pretty easy so far, right?
Importance of the Jacobian in creating Aerospace structures and fluid flow.
Now that you know the basics of algebra from 3rd year math undergrad classes, let’s delve into why it is important. I will stick to simple examples with simple ideas to explain how we can use transformations and create a much more robust aircraft that stands upto standards, principles and objectives we set.
First, lets assume a cube. A cube is just 6 squares stuck to each other. Let’s name the square Donald. This assumes that the cubes front face’s left corner is at 0.
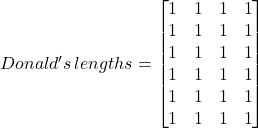
Now, let’s see what happens if we want to change this square to a sphere.
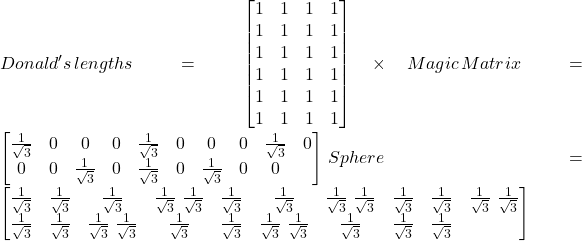
So you see that multiplying two matrices can result in a third matrix that is a completely different shape.
Let’s Connect the dots!
Now, for any aircraft to be excellent in flying, you can assume the flying as not just an interaction between mechanics, fluids, and thrust, but all of these as just values. The rate at which these affect each other, the “coefficients”, are just simple operations like multiplication and division. If you stack all of these matrices in place of the number and the coefficients multiplied, it’s called the tensor product. You will often see this as ![]() it is also called the Kronecker Product. The tensor product is useful when you want to minimize a drag over a certain region or over a certain area. Or you want to increase lift.
it is also called the Kronecker Product. The tensor product is useful when you want to minimize a drag over a certain region or over a certain area. Or you want to increase lift.
In the next few articles, we will look into the math behind using math as tool rather than as a calculator to well, calculate (the irony is just crazy) the best dimensions, factors, geometries, topologies and shapes and other dimension analysis based methods for the most optimum flight while hauling a huge amount of load. Not to forget at fairly high speed.

Leave a Reply